提出问题：想知道北京大学所有男生的平均身高是否等于1.8米1、抽样（比如抽取100人作为样本）2、做出假设，假设北京大学男生总体的平均身高等于1.8米（零假设，null hypothesis）这里用假设检验来判断样本所代表的总体的均数是否等于1.8米，本质是判断零假设成立的前提下（假设总体均数等于1.8米），是否有可能抽到目前这个样本及更极端的样本。

关于假设检验的基本思想，读一下这篇你就懂了：我来尝试给你讲清统计学中的假设检验和两类错误3、基于当前零假设和当前样本，计算 z score （z值）或t score（t值），通过z值 / t值及比该数值更极端的值出现的概率来代表抽到目前这个样本及更极端的样本的概率

。其计算公式如下。

总体标准差已知则计算z值即可，但大多数情况下总体标准差是未知的，此时用样本标准差代替，计算t值在本例中，先计算样本均数和样本标准差，即sample mean和sample standard deviation，也就是说z值和t值都是在当前抽到的样本的基础上计算得到的，如果重新抽样，z值和t值可能会变化；。

true mean under null hypothesis就是我们零假设中设定的1.8米，也就是说z值和t值都是在零假设成立的前提下计算得到的数值；true standard deviation是北京大学所有男生这个总体身高的标准差，需根据实际情况判断是否能够获得这一数据进而决定用z值还是t值。

4、在计算完z值或t值之后，如何判断z值 / t值及比该数值更极端的值出现的概率有多大？什么叫做『更极端的值』？概率小到多少就认为是不可能发生呢？z值服从标准正态分布，t值服从t分布（近似正态分布的一簇曲线，均数为零），某一段分布曲线下的面积就是某一取值范围的z值 / t值出现的概率。

注意这里的表达必须是『某一取值范围的z / t值出现的概率』，因为z分布和t分布分别是z值和t值的概率分布，单个数值对应的概率是0在z分布或t分布中，随着曲线向两端延伸，其对应的z值 / t值的绝对值越来越大，此时我们认为z / t的取值越来越极端，z值 / t值及更极端的值出现的概率越来越小。

通常假设检验中认为概率小于5%的事件在一次抽样中是不可能发生的。如下图。

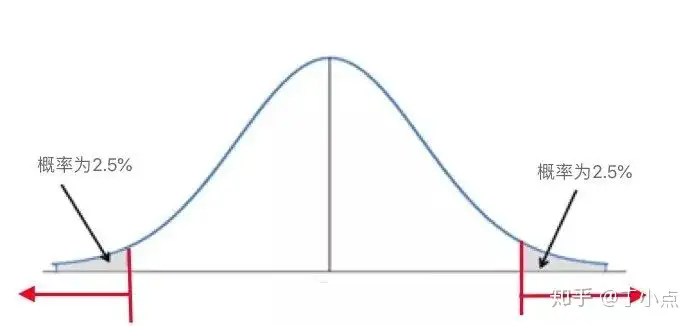
z分布或t分布曲线双侧检验红色箭头所指的横轴区域表示z值/t值及更极端的值灰色阴影部分表示z值/t值及更极端的值发生的概率，为5%也就是说，在零假设成立前提下，基于目前抽到的样本，我们的检验思路如下：计算得出的z值/t值落在红色箭头范围内

→在一次抽样中，抽中目前样本及更极端的样本的概率小于5% →在一次抽样中，目前样本及更极端的样本不可能被抽中→拒绝零假设由计算公式可知，z值和t值就是目前抽到的这个样本的均数与零假设中规定的总体均数之间的差异。

我们通常说：想判断这个差异有没有统计学意义，其实是想判断在零假设成立的前提下（假设总体均数等于1.8米），是否有可能得到目前这个样本并计算出目前这个差异『有可能得到』就是我们常说的差异没有统计学意义，还没有理由拒绝零假设；『不可能得到』就是差异有统计学意义，拒绝零假设。

本例是双侧检验，单侧检验的结论推断方法和双侧检验一样，大家可自行练习。

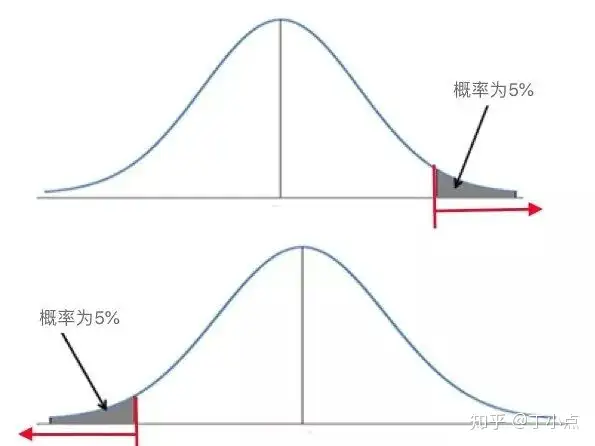
z分布或t分布曲线单侧检验的两种情况红色箭头所指的横轴区域表示z值/t值及更极端的值灰色阴影部分表示z值/t值及更极端的值发生的概率，为5%5、最后，根据目前得到的z值或t值是否落在红色箭头的范围内，得到假设检验的结论。

如果你计算得到的z或t值落在了非红色箭头的范围内，就意味着零假设成立的前提下，目前样本是有可能被抽中的（目前的样本已经被抽中了，这是事实），也就是说零假设是符合事实的，所以我们没有理由拒绝零假设相反，如果z或t值落在了红色箭头的范围内，就意味着零假设成立的前提下，目前的样本在一次抽样中是不可能发生的（这是违反事实的），那么你就有理由怀疑零假设的真实性，从而拒绝零假设。

补充：第3步中，为什么要计算z score （z值）或t score（t值），然后通过z值/t值及比该数值更极端的值出现的概率来代表抽到目前这个样本及更极端的样本的概率这一步所遵守的规律是中心极限定理即从总体中分别抽取多个样本量（样本量用n表示）足够大的样本，这些样本的均值服从正态分布。

样本均值的正态分布的均值接近总体均值，标准差为总体标准差除以根号n因此想象来自目标总体的无数个样本的均数，它们是服从正态分布的，目前被我们抽中的这个样本的均数就位于该正态分布的某一点所以要想判断目前样本均数及更极端的情况是否可能在一次抽样中被抽到，就要确定该点及更极端的情况所对应的概率大小，而正态分布曲线下面积就是概率。

为什么要计算z或t呢？因为服从正态分布的随机变量在进行简单转换后就会服从标准正态分布（其实就是按照z的计算公式经过计算后就得到了z值，z值是服从标准正态分布的），而标准正态分布的均值和标准差是唯一确定的，且其分布和密度函数也唯一，因此可以编出分布表，查出概率值。

正态分布是很重要的分布，但对每一个正态分布对应的具体概率值进行总结是不可能的，因此通常转换为标准正态分布进行查表、确定概率值，来进行数据分析和科学研究